Course announcement in English
Der Kurs findet immer im Sommersemester statt
Dozentin: Apl. Prof. Dr. Sc. Tatiana Gambaryan-Roisman
Vorlesungssprache: English
Einführung
In diesem Kurs lernen Sie eine Auswahl analytischer/mathematischer Methoden zur Lösung von Wärmeübertragungsproblemen kennen, die durch partielle Differentialgleichungen beschrieben werden können. Zu den Anwendungen gehören Wärmeleitung, konvektive Wärmeübertragung und Phasenänderungen wie Verdampfung oder Erstarrung.
Das Lernziel besteht darin, Ihnen ein leistungsfähiges und umfassendes Werkzeug an die Hand zu geben, mit dem Sie die komplexen Probleme der Wärmeübertragung und anderer Transportphänomene erfolgreich bewältigen können, auch in Kombination mit numerischen Methoden und Experimenten.
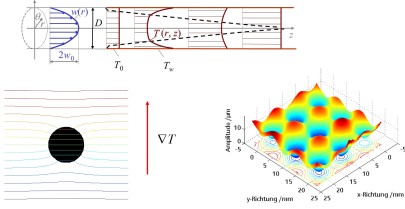
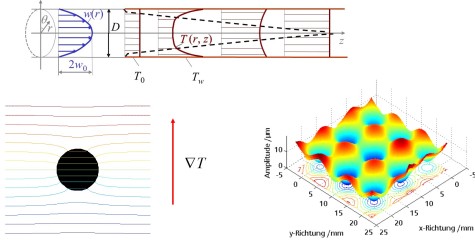
Lehrinhalte
- Einführung
- Differentialgleichungen in der Wärmeübertragung: Definitionen und Beispiele
- Methoden zur Lösung von linearen partiellen Differentialgleichungen
- Seperationsmethode
- Fourier-Reihen
- Sturm-Liouville-Probleme
- Spezielle Funktionen
- Integraltransformationen
- Einführung in die fortgeschrittenen Lösungsmethoden und Modellierung des Wärmetransports
- Störungsmethoden
- Grenzschichttheorie
- Stabilitätsanalyse
Literatur
Eine Zusammenfassung wird wöchentlich in den Vorlesungen verteilt.
Voraussetzungen
Grundkenntnisse in Mathematik und Wärmeübertragung
Online (Moodle)
Moodle: Vorlesungsfolien in Englisch und Deutsch, Skripte
Weitere Informationen: Vorlesungsankündigung Sommersemester 2025 (wird in neuem Tab geöffnet)

